Chuyên đề 5 - Chương V, Bài 2: Tổng và hiệu của hai vectơ - Toán 10 Chân trời sáng tạo

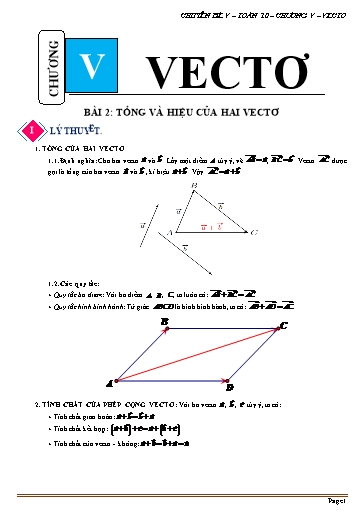
 CHUYÊN ĐỀ V – TOÁN 10 – CHƯƠNG V – VECTO
 V VECTƠ
 CHƯƠNG
 BÀI 2: TỔNG VÀ HIỆU CỦA HAI VECTƠ
I LÝ THUYẾT.
 =
 1. TỔNG CỦA HAI VECTƠ
 =    
 1.1. Định nghĩa: Cho hai vectơ a và b . Lấy một điểm A tùy ý, vẽ AB a , BC b . Vectơ AC được 
 =  
 gọiI là tổng của hai vectơ a và b , kí hiệu a b . Vậy AC a b .
 1.2. Các quy tắc:
    
 + Quy tắc ba điểm: Với ba điểm A , B , C , ta luôn có: AB BC AC .
    
 + Quy tắc hình bình hành: Tứ giác ABCD là hình bình hành, ta có: AB AD AC .
 B C
 B E C
 a Mb
 b B
 a E
 a b
 D 
 A D A
 E
 b
 2. TÍNH CHẤT CỦA PHÉP CỘNG VECTƠ: Với ba vectơ a , b , c tùy ý, ta có: q
 u
 + Tính chất giao hoán: a b b a .
 a
 + Tính chất kết hợp: a b c a b c . t
 + Tính chất của vectơ - không: a 0 0 a a . i
 o
 n
 .
 3 
 b 
 Page 1 B CHUYÊN ĐỀ V – TOÁN 10 – CHƯƠNG V – VECTO
      
 a) Ta có OA CB CO CB BO . 
 1 1 a 2
 Mặt khác BO BD a2 a2 .
 2 2 2
   a 2
 Nên OA CB .
 2
 b) Gọi A là điểm đối xứng với A qua B . 
         
 Ta có AB DC AB BA AA nên AB DC AA 2a . 
     
Câu 4. Cho bốn điểm bất kỳ A , B , C và D . Hãy chứng minh đẳng thức: AB CD AD CB .
 Lời giải
 Cách 1: Sử dụng qui tắc tổng
               
 AB CD AD DB CB BD AD CB BD DB AD CB 0 AD CB .
 Cách 2: Sử dụng hiệu hai vectơ.
           
 AB CD AD CB AB AD CB CD DB DB.
Câu 5. Cho tam giác ABC . Gọi M , N , P lần lượt là trung điểm của BC , CA , AB . Chứng minh rằng: 
    
 a) BM CN AP 0
       
 b) OA OB OC OM ON OP , với O là điểm bất kì.
 Lời giải
 A
 P N
 B
 M C
 a) Vì PN , MN là đường trung bình của tam giác ABC nên PN // BM , MN // BP suy ra tứ giác 
   
 BMNP là hình bình hành BM PN .
   
 N là trung điểm của AC CN NA.
 Do đó theo quy tắc ba điểm ta có
         
 BM CN AP PN NA AP PA AP 0 .
 b) Theo quy tắc ba điểm ta có
                
 OA OB OC OP PA OM MB ON NC OM ON OP PA MB NC
       
 OM ON OP BM CN AP 
          
 Theo câu a) BM CN AP 0 ta suy ra OA OB OC OM ON OP .
 Page 3 CHUYÊN ĐỀ V – TOÁN 10 – CHƯƠNG V – VECTO
    
 GA GD GP (đpcm).
    
 GB GC GQ (đpcm).
   
 b) Theo cách dựng hình từ đề bài ta thấy G là trung điểm PQ nên GP GQ 0.
 Biến đổi biểu thức vectơ đề cho và dựa vào kết quả câu a:
           
 GA GB GC GD GA GD GB GC GP GQ 0
Câu 9. Cho hình chữ nhật ABCD có AB 2 , AD 1. Gọi I là trung điểm CD . Hãy tính:
       
 a) AB AD BC . b) AC AB AI .
 Lời giải
 a) Ta thực hiện biến đổi:
         
 AB AD BC AB BC AD AC AD .
   
 Dựng điểm E sao cho: CE AD .
 Suy ra ACED là hình bình hành.
    
 Theo quy tắc hình bình hành: AC AD AE AE .
 Tam giác ABE vuông cân tại B nên: AE AB 2 2 2 .
 b) Ta thực hiện biến đổi:
         CD
 AC AB AI BC AI AD AI ID ID 1.
 2
     
Câu 10. Cho tam giác ABC , đặt: u AB AC ; v AB AC . Tìm điều kiện của tam giác ABC để:
 a) u v . b) u  v .
 Lời giải
 Page 5 CHUYÊN ĐỀ V – TOÁN 10 – CHƯƠNG V – VECTO
      
 An 1 An An 2 An 1 An 3 An 2 ... A2 A3 A1 A2 .
 Lời giải
      
 A A A A A A ... A A A A
 n 1 n n 2 n 1 n 3n 2 2 3 1 2
 A1 A2 A2 A3 ... An 3 An 2 An 2 An 1 An 1 An
       
 Do đó An 1 An An 2 An 1 An 3 An 2 ... A2 A3 A1 A2 A1 An .
Câu 5. Cho tam giác ABC . Bên ngoài của tam giác vẽ các hình bình hành ABIJ , BCPQ ,CARS . Chứng minh 
    
 rằng RJ IQ PS 0 .
 Lời giải
          
 RJ RA AJ , IQ IB BQ , PS PC CS .
          
 RJ IQ PS RA AJ IB BQ PC CS 
       
 RA CS AJ IB BQ PC 
       
 SC CS BI IB CP PC 
    
 SS BB CC
 0
    
 Vậy RJ IQ PS 0 .
 2 BÀI TẬP TRẮC NGHIỆM.
 ==
Câu=I 1: Cho ba vectơ a , b và c khác vectơ-không. Trong các khẳng định sau, khẳng định nào sai?
 A. a b b a . B. a b c a b c .
 C. a 0 a . D. 0 a 0 .
 Lời giải
 Chọn D
 0 a a .
   
Câu 2: Cho hình bình hành ABCD . Vectơ tổng CB CD bằng
     
 A. CA . B. BD . C. AC . D. DB .
 Lời giải
 Page 7