Chuyên đề 12: Tam giác đồng dạng - Bồi dưỡng Học sinh giỏi Toán 8

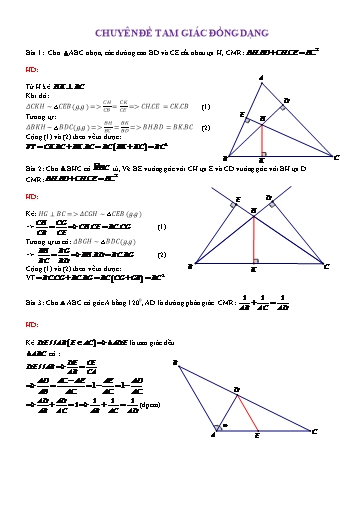
 CHUYÊN ĐỀ TAM GIÁC ĐỒNG DẠNG
 2
Bài 1: Cho ABC nhọn, các đường cao BD và CE cắt nhau tại H, CMR: BH.BD CH.CE BC
HD:
 A
Từ H kẻ HK  BC
Khi đó:
 퐾 D
훥 퐾 ∼ Δ ( . ) => = => . = 퐾. (1)
Tương tự: E
 퐾 H
훥 퐾 ∼ Δ ( . ) => = => . = 퐾. (2)
Cộng (1) và (2) theo vế ta được:
VT CK.BC BK.BC BC BK KC BC 2
 B K C
Bài 2: Cho BHC có B· HC tù, Vẽ BE vuông góc với CH tại E và CD vuông góc với BH tại D
CMR: BH.BD CH.CE BC2
HD: E D
Kẻ: ⊥ => 훥 ∼ Δ ( . ) H
 CH CG
=> CH.CE BC.CG (1)
 CB CE
Tương tự ta có: 훥 ∼ Δ ( . )
 BH BG
=> BH.BD BC.BG (2)
 BC BD
Cộng (1) và (2) theo vế ta được: B K C
VT BC.CG BC.BG BC CG GB BC 2
 1 1 1
Bài 3: Cho ABC có góc A bằng 1200, AD là đường phân giác. CMR: 
 AB AC AD
HD:
Kẻ DE / / AB E AC ADE là tam giác đều
 ABC có :
 DE CE B
DE / / AB 
 AB CA
 AD AC AE AE AD
 1 1 
 AB AC AC AC D
 AD AD 1 1 1
 1 (đpcm) 
 AB AC AB AC AD
 60
 C
 A E Bài 6: Cho ABC, M là điểm tùy ý nằm trong tam giác, đường thẳng đi qua M và trọng tâm G của tam 
 MA' MB ' MC '
giác cắt BC, CA, AB lần lượt tại A’, B’, C’, CMR : 3
 GA' GB ' GC '
HD:
Gọi AM cắt BC tại A1, Từ M vẽ đường thẳng song song với AI cắt BC tại D, 
với I là trung điểm BC
 A'M MD A
 A'GI có: MD / /GI (1)
 A'G GI
 A1M MD MD
 A1AI có MD / /GI AI 3GI (2)
 A1A AI 3GI
 A ' M 3A1M
Từ (1) và (2) ta có: 
 A 'G A1A B'
 G
 M
Chứng minh tương tự ta có: C'
 A'
 B A1 D I C
MB ' 3.B1M MC ' 3.C1M A1M B1M C1M 
 , VT 3 
GB ' B1B GC ' C1C A1A B1B C1C 
 A1M B1M C1M
mà ta có: từ bài 6 => 1 VT 3
 A1A B1B C1C
Bài 7: Cho ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H
a, CMR: AEF đồng dạng ABC
b, H là giao các đường phân giác của DEF A
c, BH.BE CH.CF BC2
HD: 1 E
 퐹 F
 2
a, Ta có: 훥 ∼ Δ 퐹 ( . ) => 퐹 = => = 
=> 훥 퐹 ∼ Δ ( . . ) H
b, Chứng minh tương tự ta cũng có:
훥 ∼ Δ , (c.g.c) và 훥 퐹 ∼ 훥 (c.g.c)
=> Do 훥 퐹 ∼ Δ => 퐹 = = 1 2
 B D C
Mà: 퐹 + 퐹 = + ( = 900) => = 퐹=> HE là phân giác góc E
Chứng minh tương tự FH là phân giác góc F, HD là phân giác góc D
c, 훥 ∼ Δ ( . ) => = => . = . (1)
và 훥 ∼ Δ 퐹 ( . ) => = 퐹 => . 퐹 = . (2)
Cộng (1) và (2) theo vế ta được đpcm Bài 12: Cho ABC và 1 điểm O thuộc miền trong của tam giác, đường thẳng đi qua O và // với AB cắt 
BC tại D và cắt AC tại G, đường thẳng đi qua O và //BC cắt AB tại K và AC tại F, đường thẳng đia qua O 
và //AC cắt AB tại H và BC tại E
 KH DE GF DG KF EH
a, CMR: 1 b, CMR: 2
 AB BC AC AB BC AC
HD: A
a, 훥 퐾 ∼ Δ . () 퐾 퐾 
 퐹 퐹 G
훥 퐹 ∼ Δ ( . ) => =
 KH DE GF KO DE OF H
Nên 1
 AB BC AC BC BC BC
 O F
b, Ta có: K
DG DC EH BE
 và , 
AB BC AC BC
 B D E C
Khi đó: 
DG KF EH DC KF BE DE EC BD EC DB DE 2BC
 2
AB BC AC BC BC BC BC BC
 NC AC
Bài 13: Cho ABC có đường trung tuyến BM cắt tia phân giác CD tại N, CMR : 1
 ND BC
HD:
 A
Vẽ DE / / BM ( E AC )
 NC MC
 QDE có NM / /DE (*) E
 ND ME
 AD AC
 ABC có DC là tia phân giác nên: (1) M
 DB BC D
 AD AE
và ABM có DE//BM (2)
 DB EM N
 AC AE 1
Từ (1) và (2) ta có : (**) 2
 BC ME B C
 NC AC MC AE ME
Lấy (*) - (**), ta có : 1
 ND BC ME ME ME
 DB EC FA
Bài 14: Cho ABC có các đường phân giác AD, BE, CF, CMR: . . 1
 DC EA FB
HD: A
 DB AB
 ABC có AD là tia phân giác nên: , 
 DC AC
 EC BC FA AC E
Tương tự: , , F
 EA AB FB BC
 Nhân theo vế ta được đpcm
 B D C
Bài 15: Cho HBH ABCD đường thẳng a đi qua A lần lượt cắt BD, BC, DC tại E, K, G 
CMR: Bài 17: Cho ABC, M là điểm nằm trong ABC, Gọi D là giao điểm của AM và BC, E là giao điểm 
của BM và CA, F là giao điểm của CM và AB, đường thẳng đi qua M và // với BC cắt DE, DF lần lượt tại 
K và I, CMR : MI=MK
HD: A
Gọi IK cắt AB. AC lần lượt tại N và Q
 AN MN
 ABD có MN / /BC 
 AB BD
 AN NQ MN NQ
 ABC có NQ / /BC (1) F
 AB BC BD BC E
 IM FM M
 FDC có IM / /DC , N H
 DC FC I K
 MN FM
 FBC có NM / /BC 
 BC FC
 IM MN IM DC
 (2) B C
 DC BC MN BC D
 IM DC.NQ DC.NQ.BD
Nhân (1) và (2) theo vế ta được: IM (*)
 BD BC 2 BC 2
Tương tự ta cũng có:
 MQ AQ NQ AQ
 ADC có MQ / /DC và ABC có NQ / /BC 
 DC AC BC AC
 MQ NQ
Do đó: (3)
 DC BC
 MK EM MQ ME
Và: EBD có MK / /BD , EBC có MQ / /BC 
 BD EB BC EB
 MK MQ MK BD
Do đó: (4)
 BD BC MQ BC
 MK NQ.BD DC.NQ.BD
Nhân (3) với (4) ta được: MK (**)
 DC BC 2 BC 2
Từ (*) và (**) ta có MI = MK
Bài 18: Cho ABC, các đường trung tuyên BM, CN cắt nhau tại G, K là điểm trên cạnh BC, đường 
thẳng qua K và // CN cắt AB ở D, đường thẳng qua K và // với BM cắt AC ở E, Gọi I là giao điểm của 
KG và DE, CMR: I là trung điểm của DE
HD: A
Gọi DK cắt BG tại H, KE cắt GC tại O và GK cắt HO tại J
 HK / /GO
Tứ giác HGOK có: => HGOK là hình bình hành
 HG / /KO
=> J là trung điểm của HO => HJ=OJ
 DH BH N M
 BNG có DH / /NG (1)
 NG BG G
 HK BH E
 BGC có HK / /GC (2)
 D I
 GC BG O
 DH HK DH NG 1 J
Từ (1) và (2) ta có (*) H
 NG GC HK GC 2
 B K C
 OE OC
CMTT ta có: CMG có OE / /GM (3)
 GM CG
 OK OC
 CBG có OK / /BG (4)
 GB CG
 OE OK OE GM 1
Từ (3) và (4) => (**)
 GM GB OK GB 2